DFS and BFS

Introduction

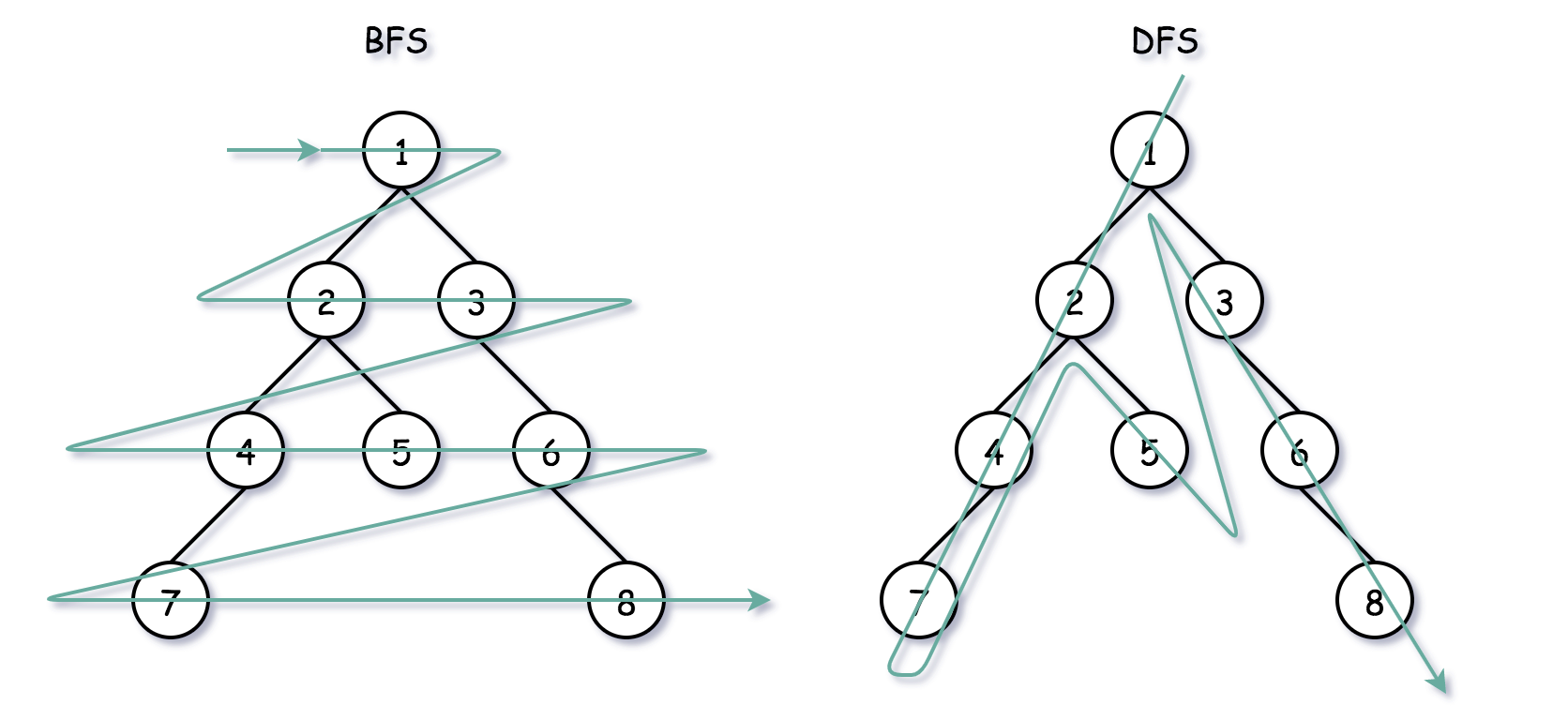
When it comes to traversing or searching through a graph or a tree, two popular algorithms come to mind: Depth-First Search (DFS) and Breadth-First Search (BFS). Both algorithms play a fundamental role in various fields, such as computer science, data analysis, network routing, and artificial intelligence. In this article, we will explore the concepts of DFS and BFS, discuss their implementations, analyze their time complexities, and provide real-time examples to better understand their differences and use cases.

Depth-First Search(DFS)

DFS is an algorithm that explores as far as possible along each branch before backtracking. It starts at a designated node and follows each path to its deepest level before moving to the next branch. DFS uses a stack to keep track of visited nodes.

• Implementation

  • Recursive Approach

    1. Start from a given node.

    2. Mark the node as visited.

    3. Recursively visit all unvisited adjacent nodes.

        # Graph representation using adjacency list
        graph = {
            'A': ['B', 'C'],
            'B': ['D', 'E'],
            'C': ['F'],
            'D': [],
            'E': ['F'],
            'F': []
        }
       
        visited = set()
       
        def dfs_recursive(node):
            visited.add(node)
            print(node, end=' ')
       
            for neighbor in graph[node]:
                if neighbor not in visited:
                    dfs_recursive(neighbor)
       
        # Usage
        dfs_recursive('A')
       

  • Iterative Approach

    1. Start from a given node.

    2. Create an empty stack and push the starting node onto it.

    3. While the stack is not empty, pop a node from the stack, mark it as visited, and push its unvisited adjacent nodes onto the stack.

        def dfs_iterative(start):
            visited = set()
            stack = [start]
       
            while stack:
                node = stack.pop()
                if node not in visited:
                    visited.add(node)
                    print(node, end=' ')
       
                    for neighbor in graph[node]:
                        if neighbor not in visited:
                            stack.append(neighbor)
       
        # Usage
        dfs_iterative('A')
       

Breadth-First Search (BFS)

BFS is an algorithm that explores all the vertices of a graph or tree in breadth-first order, i.e., it explores all the vertices at the same level before moving to the next level. BFS uses a queue to keep track of visited nodes.

• Implementation

  1. Start from a given node.

  2. Create an empty queue and enqueue the starting node.

  3. While the queue is not empty, dequeue a node, mark it as visited, and enqueue its unvisited adjacent nodes.

      from collections import deque
     
      def bfs(start):
          visited = set()
          queue = deque([start])
     
          while queue:
              node = queue.popleft()
              if node not in visited:
                  visited.add(node)
                  print(node, end=' ')
     
                  for neighbor in graph[node]:
                      if neighbor not in visited:
                          queue.append(neighbor)
     
      # Usage
      bfs('A')
     

Time Complexity

The time complexity of DFS and BFS is O(V + E), where V represents the number of vertices and E represents the number of edges in the graph or tree.

Differences between DFS and BFS

1. Traversal Order

   DFS explores as far as possible along each branch before backtracking, while BFS explores all vertices at the same level before moving to the next level.

2. Memory Usage

   DFS uses a stack to store visited nodes, while BFS uses a queue. This results in different memory usage patterns.

3. Path Finding

   DFS is typically used to find any path from the source node to the target node, while BFS is used to find the shortest path between two nodes.

4. Use Cases

   DFS is often used in maze-solving, cycle detection, and topological sorting problems, while BFS is suitable for finding the shortest path, network traversal, and web crawling.